Razones trigonométricas de ángulos agudos

Las razones trigonométricas de ángulos agudos son funciones que relacionan los ángulos de un triángulo rectángulo con las longitudes de sus lados. Estas razones son esenciales en la trigonometría y se usan ampliamente en matemáticas, física e ingeniería.

En un triángulo rectángulo, uno de los ángulos es de 90 grados, y los otros dos son agudos (menos de 90 grados). Vamos a trabajar con uno de estos ángulos agudos, llamémoslo θ. Supongamos que el triángulo rectángulo tiene los siguientes lados:

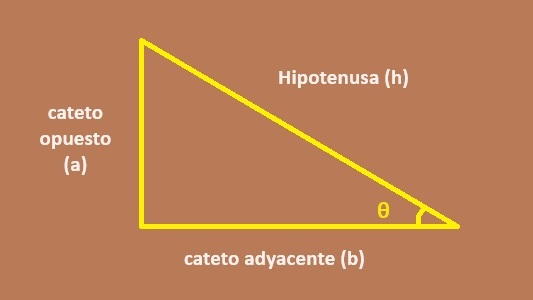
• Hipotenusa (h): El lado opuesto al ángulo recto, y el más largo del triángulo.
• Cateto opuesto (a): El lado opuesto al ángulo θ.
• Cateto adyacente (b): El lado que está junto al ángulo θ.

Las principales razones trigonométricas son:

1. Seno (sen):

El seno de un ángulo agudo θ se define como la razón entre la longitud del cateto opuesto al ángulo y la hipotenusa.

sen (θ) = Cateto opuesto/Hipotenusa = a/h

2. Coseno (cos):

El coseno de un ángulo agudo θ se define como la razón entre la longitud del cateto adyacente al ángulo y la hipotenusa.

cos(θ) = Cateto adyacente/Hipotenusa=b/h

3. Tangente (tg):

La tangente de un ángulo agudo θ se define como la razón entre la longitud del cateto opuesto al ángulo y el cateto adyacente.

tg(θ) = Cateto opuesto/Cateto adyacente = a/b

Razones Recíprocas

Además de estas tres razones básicas, existen otras tres que son recíprocas de las anteriores:

4. Cosecante (csec):

La cosecante de un ángulo agudo θ es el recíproco del seno.

csec(θ) = 1/sen(θ) = Hipotenusa/Cateto opuesto = h/a

5. Secante (sec):

La secante de un ángulo agudo θ es el recíproco del coseno.

sec(θ) = 1/cos(θ) = Hipotenusa/Cateto adyacente = h/b

6. Cotangente (ctg):

La cotangente de un ángulo agudo θ es el recíproco de la tangente.

ctg(θ) = 1/tg(θ) = Cateto adyacente/Cateto opuesto = b/a

Ejemplo Práctico

Consideremos un triángulo rectángulo donde:

• La hipotenusa h=10
• El cateto opuesto a=6
• El cateto adyacente b=8

Para el ángulo θ:

Seno:

sen(θ) = a/h = 6/10 = 0.6

Coseno:

cos(θ) = b/h = 8/10 = 0.8

Tangente:

tg(θ) = a/b = 6/8 = 0.75

Cosecante:

csec(θ) = h/a = 10/6 ≈ 1.67

Secante:

sec(θ) = h/b = 10/8 = 1.25

Cotangente:

ctg(θ) = b/a =8/6 ≈1.33

Estas razones trigonométricas son fundamentales para resolver problemas de triángulos, tanto en geometría plana como en aplicaciones más avanzadas como la física y la ingeniería.

Ver calculadoras

• Seno

Te puede interesar: