Método de los mínimos cuadrados

Suponiendo que los puntos observados en la gráfica tienen una distribución rectilínea, se plantea una ecuación cuya forma general es:

Y = A + BX

Un punto de esta recta esta dado por:

Yi = A + BXi

y para N puntos (número de datos)

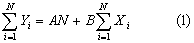
A partir de esta ecuación puede obtenerse

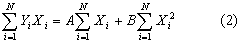
De (1) y (2) se obtienen los parámetros A y B de la recta.

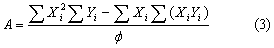
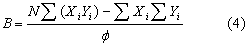
Donde:

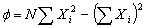
La desviación estándar de A y B se calcula en términos de la distribución de valores dYi.

dYi = Yi – (BXi + A)

Desviación estándar de A y B se calcula según:

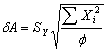
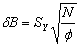
Donde:

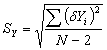
NOTA.- La aplicación del método de los mínimos cuadrados se restringe al caso especial de que toda incertidumbre se limita a la dimensión y; esto es, los valores x se conocen exactamente, o al menos con una precisión tanto mayor que los valores de y, como para despreciar la incertidumbre en la dimensión x.

Si tes gustó este sitio web puedes participar haciendo una donación voluntaria, la cual contribuirá a crecer como comunidad de Electrónicos.

o también puedes usar el código QR: